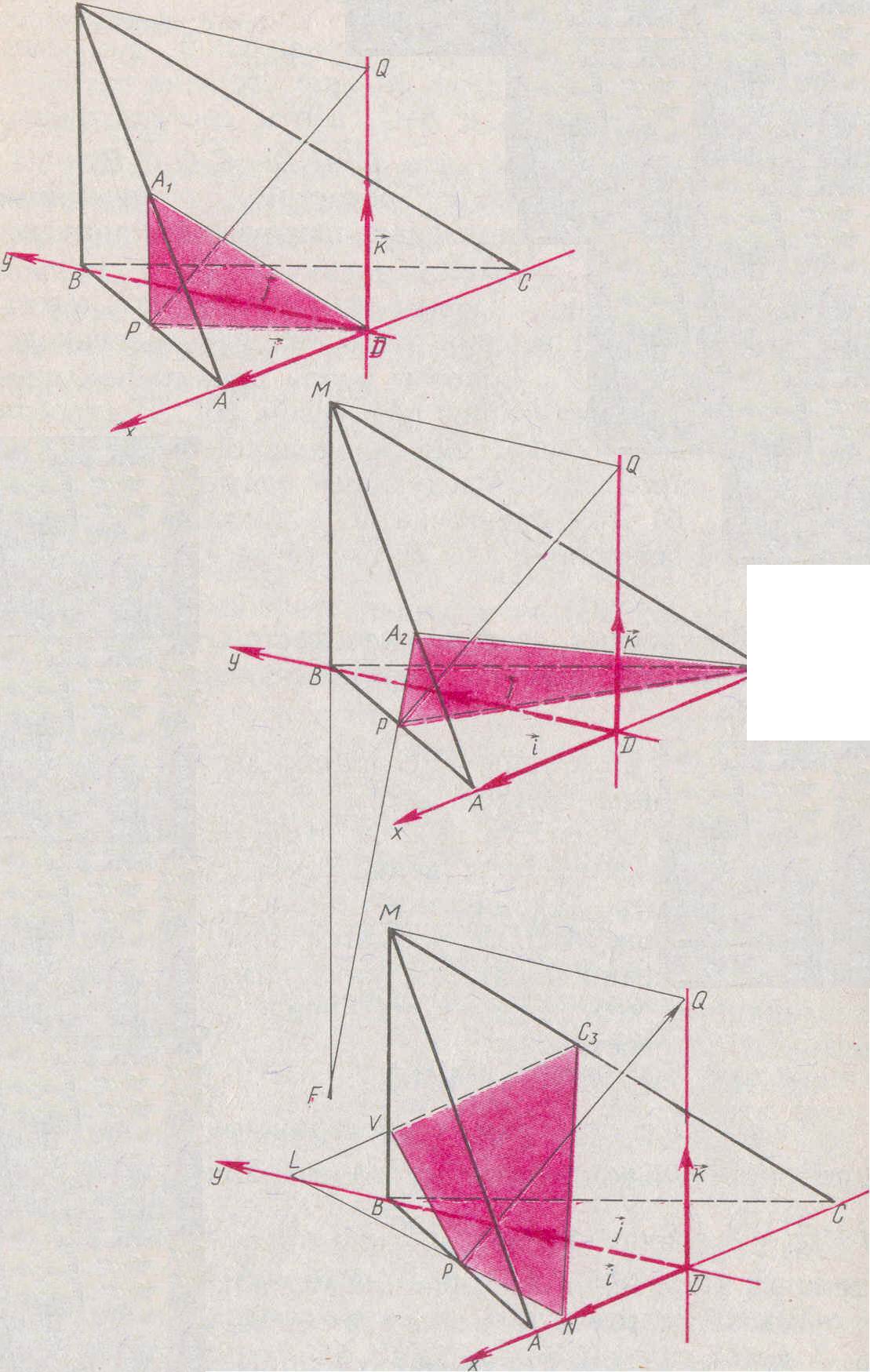
АВ и АС заданы соответственно точки Р и D - середины этих ребер. Задана также точка Q - такая, что четырехугольник МQDB является прямоугольником.

Построим сечения пирамиды плоскостями а1 а2 и а3,проходящими через прямую PQ перпендикулярно следующим плоскостям:

а) АВС, б) МАВ, в) МАС.

Решение.: Зададим в пространстве прямоугольную систему координат с началом в точке D,i=DA,j=√3/3DB, k=1/2BM. В этой системе координат D (0; 0; 0), А (1; 0; 0), В (0; √З; 0), Q (0; 0; 2).

Так как плоскости а1, а2 и а3 проходят через прямую PQ, то вектор PQ является направляющим вектором этих плоскостей.

Точка Р - середина отрезка АВ, т. е. Р (1/2; √3/2; 0) .

Тогда PQ ( -1/2; -√3/2 ; 2) . Составим теперь уравнения плоскостей аl, а2 и а3 и построим сечения пирамиды МАВС этими плоскостями.

а) Так как плоскость аl перпендикулярна плоскости АВС, то любой нормальный вектор плоскости АВС является направляющим вектором плоскости аl. Таким вектором является, например, вектор DQ (0; 0; 2).

Итак, PQ (-1/2;-√3/2;2) и DQ (0, 0, 2) – направляющие векторы плоскости аl. Тогда, если вектор n1 (k1; L1; m1) является нормальным вектором плоскости аl, то

K1*(-1/2) +L1*(-√3/2)+m1*2=0

К1*0+L1*0+ml*2=0,

откуда m1=0, и, полагая, например, L1=√З, находим, что k1=-3. Таким образом, n1(-3;√З;о).

Составим теперь уравнение плоскости аl, проходящей через точку Q (0; 0; 2) и имеющей вектор n1 своим нормальным вектором:

(x-o) (-3) + (у-о)*√3+ (z-2)*0=0, или, после упрощений: 3x-√3у=0.

Плоскость аl проходит через точки Р и Q. Как видно из уравнения плоскости аl, она параллельна оси Dz, т. е. и прямой ВМ. Построим сечение пирамиды этой плоскостью. В сечении получаем треугольник DPA1.

б) Так как плоскость а2 перпендикулярна плоскости МАВ, то любой нормальный вектор плоскости МАВ является направляющим вектором плоскости а2. Таким вектором является, например, вектор СР.

Так как С (-1;0;0) и P(1/2;√3/2;0), то CP(3/2; √3/2;0).

Таким образом PQ(-1/2;- √3/2;2) и CP(3/2; √3/2;о) - направляющие векторы плоскости а2. Тогда, если вектор n2 (k2; L2; m2) является нормальным вектором плоскости а2, то

k2*(-1/2) +L2*(-√3/2)+m2*2=0

k2*3/2 +L2*√3/2 +m2*0=0,

откуда, полагая, например, L2=2√3, находим, что k2=-2, m2=1. Таким образом, n2(-2; 2√3; 1).

Составим теперь уравнение плоскости а2, проходящей через точку Q (0; 0; 2) и имеющей вектор n2 своим нормальным вектором:

(х-0)*(-2)+(у-0)*2√З+(z-2) *1=0,

или, после упрощений 2x-2√3y-z+2=0

Плоскость a2 проходит через точки Р и Q. Ясно, что так как прямая СР параллельна плоскости a2 и точка Р лежит в плоскости a2, то плоскость a2 проходит через прямую СР.

Проще всего построить сечение пирамиды плоскостью а2, если найти еще точку пересечения ее с прямой ВМ.

Ясно, что, если F=ВМ∩а2, то F (0;.√3; f). Подставляя координаты точки F в уравнение плоскости а2, находим, что f=-4. Таким образом, Р(О; √3; -4).Построив точку Р, получаем и прямую PF - след плоскости a2 на плоскости АВМ. Получаем точку А2=РF∩МА и затем треугольник СА2Р - искомое сечение.

в) Так как плоскость а3 перпендикулярна плоскости МАС, то любой нормальный вектор плоскости МАС является направляющим вектором плоскости а3. Найдем такой вектор.

Если n (k; L; m) - нормальный вектор плоскости МАС, то n┴CA и n┴CМ. Так как в заданной системе координат С (-1; 0; 0) и М (0; √3; 2), то СА (2; 0; 0) и см (1; √3; 2). Тогда

k*2+L*0+m*0=0,

k*1 +L*√3+m*2=0,

откуда k=O, и, полагая, например, L=√3, находим m=-3/2 . Таким образом, n (0; √3; -3/2 ).

Итак, PQ (- 1/2 ; - √3/2 ; 2) и n (0; √3; - 3/2) - направляющие векторы плоскости а3. Поэтому, если вектор nз (kз; Lз; mз) является нормальным вектором плоскости а3, то

kз*(-1/2) +L3*(- √3/2) +mз*2=0

kз*0+L3*√3+m3*(-3/2) =0,

откуда, полагая, например, L3=√3, находим m3=2, k3=5.

Таким образом, n3 (5; √3; 2), и мы получаем следующее уравнение плоскости аз: - .

(х-0)*5+ (у-0)* √3+ (z-2)*2=0,

или, после упрощений 5x+√3y+2z-4=0..

Для построения сечения пирамиды плоскостью а3 найдем точки пересечения плоскости а3, например, с прямыми DB и МВ.

Если а3∩DВ =S, то S (0; 1; 0). Подставляя координаты точки S в уравнение плоскости а3, находим, что L=4*√3/3. Построим точку s по ее координатам.

Аналогично, если а3∩МВ=V, то V(0; √3; v), и, подставляя координаты точки V в уравнение плоскости а3, находим, что v=1/2 .

Построим точку V (0; √3; 1/2) по ее координатам, а затем построим сечение пирамиды плоскостью а3, проходящей через точки Р, L и V. в сечении получаем четырехугольник РVСзN.