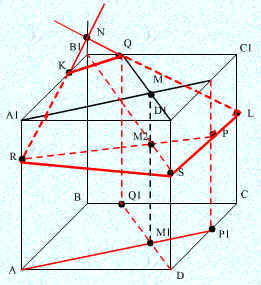
2. Метод внутреннего проектирования
Этот метод удобен при построении сечений в тех случаях, когда почему-либо неудобно находить след секущей плоскости, например, след получается очень далеко от заданной фигуры
ПРИМЕР. Точки P, Q и R взяты на поверхности параллелепипеда ABCDA1B1C1D1 следующим образом: точка Р лежит на грани CC1D1D точка - на ребре ВС1, а Q точка - на ребре АА1. Построим сечение параллелепипеда плоскостью PQR.
РЕШЕНИЕ Пересечение секущей плоскости с плоскостью АВС (т.е. след секущей плоскости на плоскости АВС) не помещается на нашем изображении. Можно было бы, конечно, найти след секущей плоскости на плоскости какой-нибудь другой грани, например на плоскости ВВ1С1. (Для этого нужно было бы найти проекции точек Р и R на плоскость ВВ1С1 а затем найти точку Х - точку пересечения прямых PR P1R1. Тогда прямая XQ - искомый след.) Мы, однако, применим здесь метод внутреннего проектирования. При построении сечения этим методом не требуется находить след секущей плоскости. Выполним нужные построения в следующем порядке.
Построим плоскость АА1РР1, определяемую параллельными прямыми АА1 и РР1 и плоскость DD1QQ1, определяемую параллельными прямыми QQ1 и DD1.
найдем прямую ММ1, по которой пересекаются две построенные плоскости.
Найдем точку М2, в которой пересекаются прямые PR и MM1.
В плоскости DD1QQ1 проведем прямую QM2 и найдем точку S - точку ее пересечения с прямой DD1.
Итак, на ребре DD1 найдена точка, принадлежащая секущей плоскости. Далее, легко находятся точки пересечения других ребер с секущей плоскостью.
В плоскости СС1D1 проведем прямую SP и найдем точку L, в которой пересекаются прямые SP и CC1.
В плоскости ВВ1С1 проведем прямую RN и найдем точку N, в которой пересекаются прямые QL и BB1.
В плоскости АА1В1 поведем прямую RN и найдем точку K, которой она пересекаются с прямой АВ1.
Соединим точки К и Q, R и S. Многоугольник RSLQK - искомое сечение.