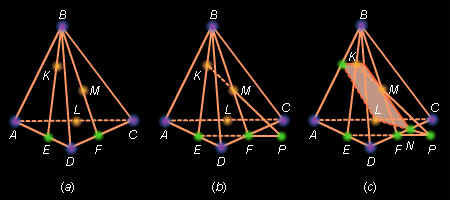
1.2 метод вспомогательных сечений

Здесь точки K, L и M лежат на гранях ABD и BCD, а точка L – на ребре AC. Естественно, что сразу построить «след» плоскости сечения нельзя. Рассмотрим вспомогательную плоскость BMK. В этой плоскости уже можно построить прямую KM – «след» сечения. Пусть P – точка пересечения прямых KM и EF. Точка P лежит в плоскости ADC и в плоскости сечения. Однако в этой же плоскости лежит и точка L. Проведем прямую LP – «след» сечения в плоскости ADC, получаем точку N и достраиваем сечение.

Рассмотрим теперь общий случай, когда все три точки, задающие сечение, лежат на плоскостях граней, но не на ребрах пирамиды 

Проведем вспомогательную плоскость DKM, пересекающую ребра AB и BC в точках E и F. Теперь построим «след» KM плоскости сечения на этой вспомогательной плоскости и найдем точку пересечения прямых KM и EF – точку P. Так как точки P и L лежат в плоскости ABC, то можно провести прямую, по которой плоскость сечения пересекает плоскость ABC. Теперь можно достроить сечение.

Проиллюстрируем еще один метод построения сечений, который называется методом внутреннего проектирования. Его особенность заключается в том, что с его помощью можно строить сечения, «находясь внутри» многогранника.

Построим вспомогательную плоскость BLC и в ней отрезок LM . Построим еще одну вспомогательную плоскость DCK. BLDK = E. Точка E при этом принадлежит обеим вспомогательным плоскостям. Пусть LMEC = F. Точка F лежит в плоскости сечения и в плоскости DCK. Теперь проведем прямую KF и найдем точку пересечения этой прямой с DC – точку N, которая тоже принадлежит сечению. Тогда четырехугольник KLNM и будет искомым сечением.

Можно поступить по-другому и начать с конца. Допустим, что искомое сечение KLNM построено.

Пусть F – точка пересечения диагоналей четырехугольника KLNM. Проведем прямую DF и обозначим через F1 точку пересечения с гранью ABC. Точка F1 одновременно принадлежит плоскостям AMD и DCK и потому совпадает с точкой пересечения прямых AM и CK, эту точку легко построить. Далее строим точку F как точку пересечения DF1 и LM. Затем находим точку N.