В этом разделе представлены основные понятия, аксиомы и теоремы, используемые при построении сечений.

Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Они образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.
Из всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, правильные многогранники и их разновидности.
Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой. Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.

Многогранник, у которого одна из граней – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называются пирамидой. Грань–многоугольник называют основанием призмы, а треугольники – боковыми гранями пирамиды. Общая вершина треугольников называется особой вершиной пирамиды (обычно, просто вершиной).
Под изображением многогранников на чертеже будем понимать изображение ограничивающей его многогранной поверхности, т.е. изображение совокупности составляющих ее многогранников.
Геометрическая фигура, получающаяся в результате пересечения многогранника плоскостью, называется сечением многогранника.
![]()
Сечение представляет собой плоский многоугольник с внутренней областью. В частном случае эти многоугольники могут распадаться на несколько многогранников, вырождаться в прямые и точки.
Сечение многогранника плоскостью можно построить двумя способами:
1. По точкам пересечения с плоскостью ребер многогранника.
2. По линиям пересечения граней многогранника с плоскостью.
В первом случае задача сводится к определению точек пересечения прямой с плоскостью. Во втором случае - к определению линий пересечения плоскостей.
В ряде случаев целесообразно комбинированное применение обоих способов.
В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается еще одна основная фигура - плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
Как и ранее, точки будем обозначать прописными латинскими буквами А, В, С и т. д., а прямые - строчными латинскими буквами а, Ь, с И т. д. или двумя прописными латинскими буквами АВ, CD и т. д. Плоскости будем обозначать греческими буквами а, Р, Y и т. д. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области.
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, большая часть которых нам знакома по курсу планиметрии. Мы сформулируем лишь три аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве.
А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Плоскость, проходящую через точки А, В и С, не лежащие на одной прямой, иногда называют плоскостью ABC. Отметим, что если взять не три, а четыре произвольные точки, то через них может не проходить ни одна плоскость. Иначе говоря, четыре точки могут не лежать в одной плоскости. Каждый знаком с таким наглядным подтверждением этого факта: если ножки стула не одинаковые по длине, то стул стоит на трех ножках, т.е. опирается на три "точки", а конец четвертой ножки (четвертая "точка") не лежит в плоскости пола, а висит в воздухе.
А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
В таком случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
Свойство, выраженное в аксиоме А2, используется для проверки "ровности" чертежной линейки. С этой целью линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный (прямолинейный), то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.
Из аксиомы А2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
В таком случае говорят, что плоскости пересекаются по прямой. Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.
Первые следствия из аксиом стереометрии
Теорема 1.1.
Через прямую и точку вне ее можно провести плоскость, и притом только одну.
Теорема 1.2.
Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
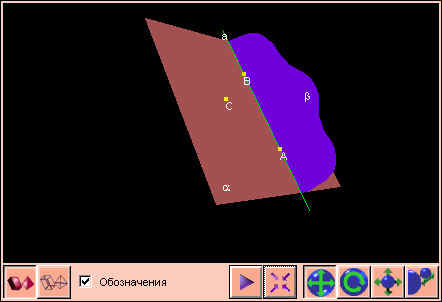
Плоскость и прямая вне ее либо не имеют общих точек, либо имеют единственную общую точку.
Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Параллельность прямой и плоскости
Определение
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Если прямая a параллельна плоскости α, то пишут a || α.
Теорема Признак параллельности прямой и плоскости.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
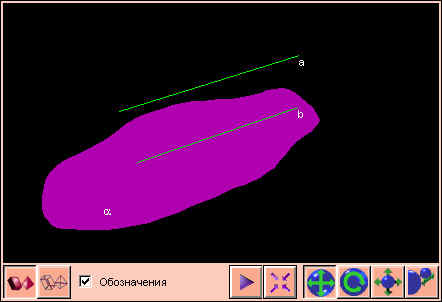
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.
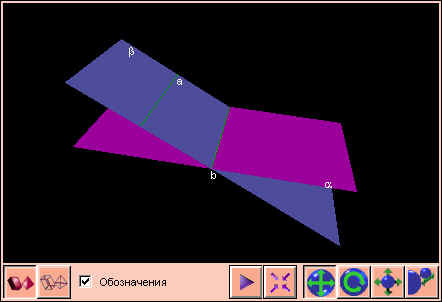
Прямую b иногда называют следом плоскости β на плоскости α.
Параллельность двух плоскостей
Определение
Две плоскости называются параллельными, если они не имеют общих точек.
Теорема Признак параллельности плоскостей.
Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны.
Теорема :
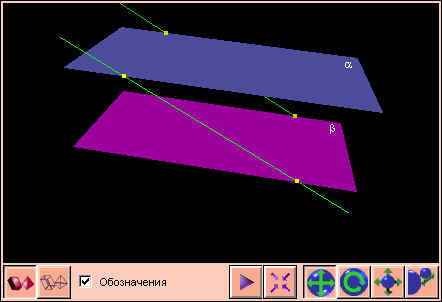
Если две параллельные плоскости пересечены третьей, то она оставляет на этих плоскостях параллельные следы.
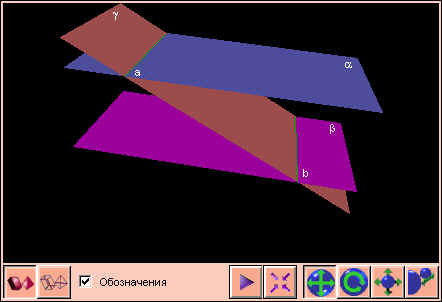
Теорема
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Теорема
Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны.
Теорема
Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях.
Угол между двумя скрещивающимися прямыми
С появлением в стереометрии скрещивающихся прямых возникает вопрос: как определить угол между двумя скрещивающимися прямыми?
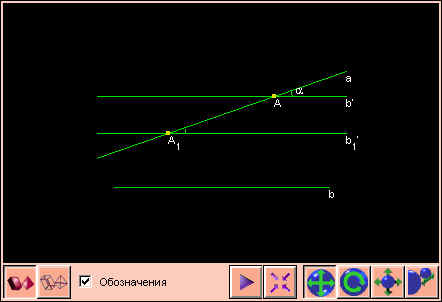
Пусть прямые a и b скрещивающиеся. Выберем на прямой a произвольную точку A. Проведем через нее прямую b' || b. Угол между прямыми a и b' по теореме 2.10 равен углу между скрещивающимися прямыми a и b. Ясно, что величина этого угла не зависит от выбора точки A. Действительно, выберем на прямой a точку A1 ≠ A и проведем через нее прямую b1' ||b. Поскольку b` || b и b1' || b, то b1' || b'. Прямые b' и b1' образуют с прямой a одинаковые углы.
Определение
Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Определение
Две прямые в пространстве называются перпендикулярными, если они образуют прямой угол. На чертеже изображен куб ABCDA1B1C1D1. Скрещивающиеся прямые A1D1 и CD перпендикулярны. Действительно, A1D1 C1D1, а C1D1 || CD.
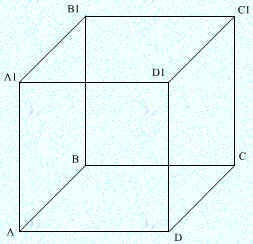
Назовем еще несколько пар скрещивающихся перпендикулярных прямых: A1D1 и AB, A1B1 и BC, A1B1 и AD, B1C1 и AB.
Перпендикулярность прямой и плоскости
Определение
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
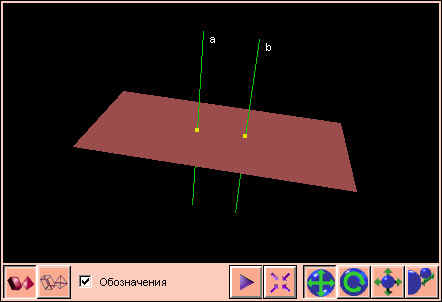
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Две плоскости, перпендикулярные одной прямой, параллельны между собой.

Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной данной плоскости, который соединяет данную точку с точкой плоскости.

Пусть AO – перпендикуляр к плоскости α, O – основание перпендикуляра. Длина этого перпендикуляра AO называется расстоянием от точки A до плоскости α. Отрезок, соединяющий точку A с любой точкой плоскости, отличной от O, называется наклонной (AB – наклонная, B – основание наклонной, BO – проекция наклонной на плоскость α).
Если из одной точки вне плоскости проведены к ней перпендикуляр и наклонные, то длина перпендикуляра меньше длины любой наклонной;
наклонные с равными проекциями равны;
из двух наклонных большую длину имеет та, у которой больше проекция.
О трех перпендикулярах.
Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость.
Теперь можно приступить к изучению способов построения сечений